江苏行测数量关系，比较构造法解应用题
江苏公务员行测数量关系技巧 行测解答都有很多方向技巧，那么，接下来就由小编为大家介绍一种在日常备考中，针对数量关系应用题比较实用的技巧，比较构造法解。
例题讲解，做好笔记 一、什么是比较构造法？
对同一事物可以对同一事物可以采取两种不同的分配方案，比较两种方案间的异同，建立方案之间的联系，构造关系式，这就是比较构造法。
那么到底如何利用比较构造法来解题呢？下面我们一起来看一下！
【经典例题】：学校第一次买来15个凳子和6把椅子共付318元。若第二次买来同样的凳子8个和同样的椅子6把共付234元，求凳子的单价？
解析：我们会发现题干中给出两个不同的买凳子和椅子的方案，且花了不同的总价钱，我们可以列出来比较一下。
通过表格我们会发现买的椅子数量是一样的，所以总价所减少的钱数就相当于少买的15-8=7个凳子所省下来的钱数，即：7×凳子单价=318-234，可求出凳子单价为12元/个。
(通过对上面这道题的分析，我们可以总结出比较构造法的大致解题思路。)
二、解题思路
1.列出题干中所给的不同方案；
2.比较方案之间的差异；
3.根据差异建立联系求解。
三、常见应用
(一)已知两种不同方案
例1：给贫困学校送一批图书，如果每所学校送80本书，则多出了340本；如果每所学校校送90本书，则少60本。问共有多少图书？
【解析】①列出方案
②比较差异
我们会发现两个方案间每所学校得到的书是不相同的，也就是说两种方案所有学校的图书需求量是不同的，如果想让每所学校得到的书从80本变成90本(即每所学校在原有80本书的基础上多10本)，则需要340+60=400本。
③求解 因此，学校数量=400÷10=40所。
例2：有一项工程甲公司花6天，乙公司再花9天可以完成，或者甲公司花8天，乙公司再花3天可以完成，如果这项工程由甲或乙单独完成，则甲公司所需天数比乙公司少多少天？
【解析】①列出方案
②比较差异
由上表可知，甲工作2天相对于乙工作6天，即在做同一工程中，甲和乙的效率比是3:1，则可直接设甲的效率为3，乙的效率为1，因此总工作量为6×3+9=27。
③求解因此，所求为27-(27÷3)=18天。
例1：班级男生人数是女生人数的2倍，现排值日生轮流表，若每班排男生3人，女生2人，则最后剩男生6人，问班级共有多少名学生？
【解析】①列出方案
分析如何构造方案：根据题中所给的比例关系以及剩余人数构造理想方案。 我们会发现，如果我们按照题中所给的男女生人数的比例关系去安排每天的值日生的话，那么到最后一天应该会刚好安排完所有人，也就是说剩余人数为0，而对于实际方案来讲剩余了6个男生，所以可以让每天安排女生的人数不变仍然是2，则理想方案每天安排男生人数为4，此时对于每天安排的男生人数就出现了差异，再通过比较差异，进行求解。
②比较差异
通过上表可知，如果想让每天值日的男生人数都多1个人的话，那么需要6个男生，则需要值日的天数为6天
③求解因此，班级总人数为(3+2)× 6+6=36人。
例2：车间领到一批电影票和球票发放给车间工人，电影票是球票数的2倍。如果每个工人发3张球票，则富余2张，如果每个工人发7张电影票，则缺6张。问车间领到多少张球票？
【解析】①列出方案
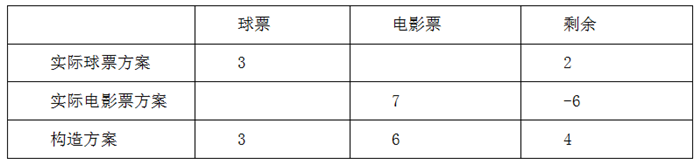
分析如何构造方案：根据题中所给电影票与球票2：1的比例关系，若让电影票票数不变，则球票票数根据比例关系换算会变成一个小数，不方便计算，因此我们让球票票数不变，则根据比例关系，电影票票数应为6张，剩余4张，此时对于电影票的票数就出现了差异，再通过比较差异，进行求解。
②比较差异
通过上表可知，如果每人的电影票要从7张变成6张，则需要从每人手里收回一张，共需要收回6+4=10张，则工人人数为10人。
③求解因此，车间领到球票共3×10+2=32张。
以上就是今天为大家介绍一种实用的技巧，比较构造法解应用题。希望对大家考场作答有一定帮助，最后祝大家考试顺利。
更多数量关系技巧与方法扫码获取
技巧还没掌握？扫码回复“咨询老师”
点击分享此信息：
相关文章
