江苏行测，巧用公式秒解数量关系容斥难题
江苏公务员行测数量关系技巧 今天，小编为大家分享的是行测数量关系模块的经典题型——容斥问题，帮助大家学会题型的判断和对应套路的使用，赶紧一起学起来~
例题讲解，做好笔记 容斥问题
容斥问题的本质是去除重复，而解题方法是公式法和图示法。首先优先使用公式法，两集合类容斥问题的公式为：总情况数－两个条件都不满足的个数=满足条件1的个数+满足条件2的个数-两个条件都满足的个数，能够直接套用公式的题目优先套用公式。当题目中出现“只”满足一个条件这样的字眼，由于公式当中无法直接求出，可使用图示法进行求解。
那么下面我们一起看几个例题，应用一下两集合类容斥问题的两种解题方法。
【解析】
第一步，本题考查容斥问题。
第二步，能够进入工作组的员工即为两个条件都满足的人，设能够进入工作组的员工有x人，根据两集合容斥公式：总数－都不=A+B－AB，代入数据可得80-10=40+46-x，解得x=16人。因此，选择A选项。
【解析】
第一步，本题考查容斥问题。
第二步，设两门课程都没有得满分的有x人，根据二者容斥公式可得：62+34-11+x=100，解得x=15，即两门课程都没有得满分的有15人。因此，选择B选项
【解析】
第一步，本题考查容斥问题，属于二集合容斥类，用公式法解题。
第二步，共两个兴趣小组，其中80%的学生参加地理兴趣小组、50%的学生参加生物兴趣小组，根据两集合容斥原理公式：满足条件1的个数＋满足条件2的个数－两者都满足的个数＝总个数－两者都不满足的个数，设同时参加两个兴趣小组的学生占比为x，则有80%＋50%－x＝100%－0，解得x＝30%，那么同时参加两个兴趣小组的共有300×30%＝90（人）。因此，选择C选项。
【解析】
第一步，本题考查容斥问题。
第二步，如下图：
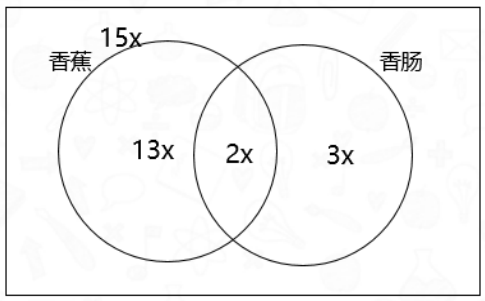
设两种食物都吃的狒狒有2x只，则只吃香肠的有3x只，根据吃香蕉是吃香肠的3倍，可得吃香蕉的有（2x＋3x）×3＝15x只，进食的狒狒共15x＋3x＝18x只，占总数的90%，共计18x÷90%＝20x只狒狒，未进食的有2x只，是只吃香蕉的2/13。
因此，选择C选项。
更多数量关系技巧与方法扫码获取
技巧还没掌握？扫码回复“咨询老师”
点击分享此信息：
相关文章
